Zeitparallelisierung über die Schritte hinweg
In den letzten zehn Jahren hat das Interesse an der Entwicklung paralleler Methoden für die zeitliche Integration gewöhnlicher Differentialgleichungen (ODEs) zugenommen, insbesondere im Zusammenhang mit zeitlichen Strategien für partielle Differentialgleichungen (PDEs). Ein Faktor, der dieses Interesse anheizt, hängt mit der Entwicklung von Supercomputern in dieser Zeit zusammen. Um eine groß angelegte Parallelisierung in der Zeit zu erreichen, können verschiedene Methoden wie Parareal, Diagonalisierung oder das parallele vollständige Approximationsschema in Raum und Zeit (PFASST) verwendet werden, um mehrere Zeitschritte gleichzeitig zu integrieren.
PFASST
Um die inhärente serielle Abhängigkeit in Zeitrichtung zu überwinden, führt PFASST eine Raum-Zeit-Hierarchie ein, bei der Integratoren mit unterschiedlichen Kosten iterativ gekoppelt werden. Serielle Abhängigkeiten werden auf die gröbste Ebene verlagert, so dass die rechenintensiven Teile auf feineren Ebenen parallel behandelt werden können. Diese Methode weist eine starke Verwandtschaft mit linearen oder nichtlinearen Mehrgitterverfahren auf und kann auf ähnliche Weise analysiert werden.
Ref: M. L. Minion, R. Speck, M. Bolten, M. Emmett, and D. Ruprecht, Interweaving PFASST and Parallel Multigrid, SIAM Journal on Scientific Computing, 37(5), 244 - 263, 2015.
Diagonalisierung
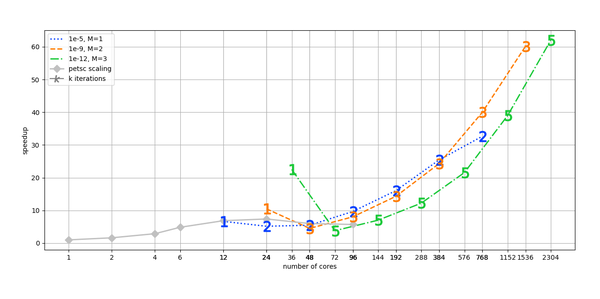
Um die Vergröberung mit all ihren Fallstricken zu vermeiden, verwenden diagonalisierungsbasierte Methoden blockzirkulierende Vorkonditionierer zur Parallelisierung der Integration von mehreren Zeitschritten. Diese Vorkonditionierer können mit Hilfe von schnellen Fourier-Transformationen (FFT) effizient in der Zeit diagonalisiert werden. Während dieser Ansatz auch für hyperbolische Probleme gut funktioniert, ist seine direkte Anwendung auf lineare Probleme beschränkt. Die wichtigste Frage in diesem Forschungsbereich ist, wie man effiziente parallele Integratoren für nichtlineare Probleme erhält.
Ref: Gayatri Caklovic, Robert Speck, Martin Frank, A parallel implementation of a diagonalization-based parallel-in-time integrator, arXiv:2103.12571 [math.NA], submitted.
Parareal für Partikel-Mesh Methoden
Bei kinetischen Plasmasimulationen wird eine hochdimensionale PDE simuliert, und Partikel-Netz-Methoden sind die bevorzugten Methoden dafür. Sie müssen in der Regel über Hunderttausende von Zeitschritten in einem langen Zeitintervall integriert werden. In dieser Forschungsarbeit beschleunigen wir kinetische Plasmasimulationen durch die zeitliche Parallelisierung der Partikel-in-Fourier-Schemata unter Verwendung des Parareal-Algorithmus. Die Schlüsselfrage, die wir zu erforschen versuchen, ist, wie die zeitliche Parallelisierung auf komplexe, nichtlineare, hochdimensionale gekoppelte PDE-Systeme mit einer großen Bandbreite an räumlichen und zeitlichen Skalen angewendet werden kann.
Ref: Sriramkrishnan Muralikrishnan, Robert Speck, ParaPIF: A Parareal Approach for Parallel-in-Time Integration of Particle-in-Fourier schemes, arXiv:2407.0085 [math.NA], submitted.