Probanden gesucht

Wir wollen, dass unsere Forschung wirkt. Deshalb arbeiten wir daran, unsere Forschungsergebnisse für Gesellschaft, Politik und Wirtschaft nutzbar zu machen und gestalten dabei die eigene Forschung durch Impulse von außen. Wir legen viel Wert auf eine enge Zusammenarbeit mit den Partnern aus der Industrie, damit aus unseren Erkenntnissen neue Produkte entstehen, die das Leben der Menschen langfristig verbessern.
PHYSIK DER MEDIZINISCHEN BILDGEBUNG (INM-4)
Die Forschungs- und Entwicklungsarbeiten unserer Institutsbereiche der Physik der Medizinischen Bildgebung (INM-4) des Instituts für Neurowissenschaften konzentrieren sich auf die Entwicklung, experimentelle Validierung und klinische Prüfung neuer Bildgebungsmethoden des Gehirns.
Institutsleitung: Univ.-Prof. Dr. Dr. h.c. N. J. Shah
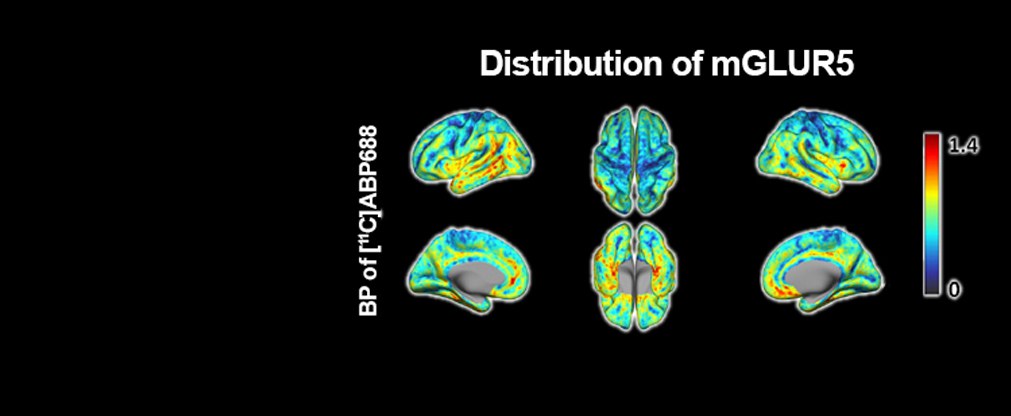
Jülicher Bildgebungstechnik ermöglicht präzise Einblicke in Struktur und Funktion des menschlichen Gehirn
Innovation - Förderung - Forschung
Probanden gesucht
Nachrichten
MELDUNGEN
2. April 2025 - Schnelle MRT-Technik zeigt Potenzial für die Beurteilung von Hirntumoren
13. December 2024 - Studie zeigt Langzeiteffekte von anodaler tDCS auf Gehirnchemie und Energiestoffwechsel
29. November 2024 - Einblicke in Depressionen durch fortschrittliche bildgebende Verfahren
27. October 2024 - Verbesserte B1-Kartierungstechnik verbessert SNR in der MRT
1. September 2024 - Ein neuartiges MRT-Verfahren für ein verbessertes Multi-Parameter-Mapping
24. Juli 2024 - 7T-MRS-Studie bringt Licht ins Dunkel der Beziehung zwischen Metaboliten im posterioren cingulären Cortex und Aufmerksamkeit
17. Juli 2024 - Einblicke in die Basalganglien-Thalamo-kortikale Konnektivität bei Major Depression mittels 7T fMRI
17. Juli 2024 - Neues gekrümmtes MRT-Spulendesign verbessert die Bildgebung von Kükenembryonen
6.Juli 2024 - Bewertung von Abschwächungskorrekturmethoden für die PET/MR-Bildgebung
20. Mai 2024 - Neue Studie unterstreicht die Bedeutung von sozialer Unterstützung und psychologischer Belastbarkeit für die funktionelle Konnektivität im Gehirn
13. Mai 2024 - Einblicke in die Veränderungen der Mikrostruktur des Gehirns über die Lebensspanne hinweg
5. April 2024 - Neue Studie zeigt verbesserte Totzeitkorrektur bei der PET-Gehirnbildgebung
15. Februar 2024 - KI-gestützte PET-Bildgebung identifiziert verborgene Hirntumorläsion
8. Februar 2024 - Überprüfung von Submillimeter-fMRI-Erfassungstechniken zur Erkennung von Hirnaktivierung auf laminarer und säulenförmiger Ebene
8. Januar 2024 - Neue Butterfly-Spule demonstriert verbesserte Signalqualität